-
Longitud necesaria de una barrera para que detenga un coche (7096)
La fuerza ejercida sobre un automóvil por una barrera parachoques al golpear el automóvil contra ésta es 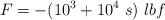 , donde s es la distancia en pies medida desde el punto de contacto inicial. Si se quiere diseñar la barrera de manera que pueda detener un auto de
, donde s es la distancia en pies medida desde el punto de contacto inicial. Si se quiere diseñar la barrera de manera que pueda detener un auto de 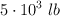 que viaje a
que viaje a 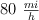 , ¿cuál será la longitud efectiva necesaria de la barrera, es decir, cuál será la distancia necesaria de la barrera para que detenga al automóvil?
, ¿cuál será la longitud efectiva necesaria de la barrera, es decir, cuál será la distancia necesaria de la barrera para que detenga al automóvil?
-
Constante elástica efectiva de dos resortes en serie (7078)
¿Cuál es el valor de la constante efectiva de dos resortes idénticos conectados en serie que está utilizando un artista para una instalación de la próxima bienal, si la constante de cada uno de ellos es de 200 N/m y sobre los cuales cuelga un determinado peso?
-
Esfuerzo de un resorte conocido su módulo de Young y su deformación (7074)
Determina el esfuerzo en un resorte con un módulo de Young equivalente a 300 Pa, si su deformación es de 30.
-
Velocidad, componentes de la aceleración y radio de curvatura a partir de vector de posición (7065)
Una mosca tiene el vector de posición 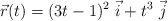 . Calcula:
. Calcula:
a) El vector velocidad instantánea y el vector aceleración instantánea para t = 5 s.
b) Los módulos de la aceleración tangencial y normal para t = 2 s.
c) El radio de curvatura para t = 2 s y la ecuación de la trayectoria.
-
Velocidad y velocidad angular de una esfera que rueda por una rampa al llegar al suelo (6891)
Una esfera de radio r = 24.5 cm y masa m = 1.20 kg parte del reposo y rueda hacia abajo sin deslizamiento sobre una rampa con  de inclinación que tiene 10.0 m de largo. Calcula las velocidades de traslación y rotación cuando llega a la parte inferior de la rampa.
de inclinación que tiene 10.0 m de largo. Calcula las velocidades de traslación y rotación cuando llega a la parte inferior de la rampa.
El momento de inercia de una esfera sólida con respecto a un eje de rotación que pasa por su centro de masa es 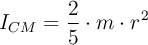 .
.
 Ejercicios FyQ
Ejercicios FyQ