-
Posición del centro de masas en el sistema Tierra-Luna (7753)
La masa de la Tierra es 81 veces mayor que la de la Luna y la distancia entre sus centros es sesenta radios terrestres (60 R). El centro de masas del sistema Tierra-Luna ocupa una posición que está:
a) Por encima de la superficie terrestre.
b) Por debajo de la superficie terrestre.
c) A la mitad de la distancia entre ambos cuerpos celestes.
d) Indeterminada, ya que depende de las fases de la Luna.
-
Dinámica de un sistema de cuerpos unidos por un muelle y una cuerda (7700)
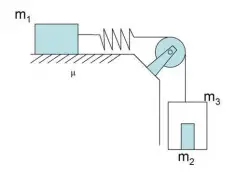
El siguiente sistema está compuesto por tres masas de igual valor 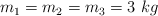 . La constante de recuperación del muelle es
. La constante de recuperación del muelle es 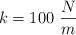 . El cuerpo
. El cuerpo 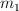 tiene coeficientes de fricción con el suelo
tiene coeficientes de fricción con el suelo 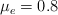 y
y 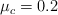 .
.
Artículos de esta sección
a) Si el sistema se encuentra en reposo: calcula la fuerza de fricción y la longitud que se estira el muelle.
b) Si el sistema se encuentra en movimiento: calcula la fuerza de contacto entre 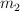 y
y 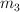 .
.
-
Inercia rotacional de una polea en un sistema de dos cuerpos unidos (7681)
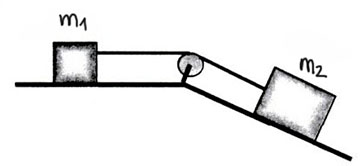
La figura muestra una masa de 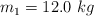 que descansa sobre una superficie horizontal lisa y que está unida a otra masa
que descansa sobre una superficie horizontal lisa y que está unida a otra masa 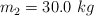 que se encuentra sobre un plano inclinado liso, que forma un ángulo de
que se encuentra sobre un plano inclinado liso, que forma un ángulo de 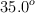 con la horizontal. Ambas masas se unen por medio de una cuerda ideal y que pasa por una polea de radio
con la horizontal. Ambas masas se unen por medio de una cuerda ideal y que pasa por una polea de radio 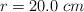 . La cuerda no desliza sobre la polea, que puede girar libremente alrededor de un eje perpendicular a la página y que pasa por su centro. Cuando el sistema se libera del reposo, la masa
. La cuerda no desliza sobre la polea, que puede girar libremente alrededor de un eje perpendicular a la página y que pasa por su centro. Cuando el sistema se libera del reposo, la masa 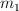 se mueve hacia la derecha con una aceleración
se mueve hacia la derecha con una aceleración 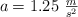 . ¿Cuál es la inercia rotacional de la polea?
. ¿Cuál es la inercia rotacional de la polea?
Artículos de esta sección
-
Tensión en la cuerda de sistema de dos cuerpos unidos, con polea con momento de inercia (7600)
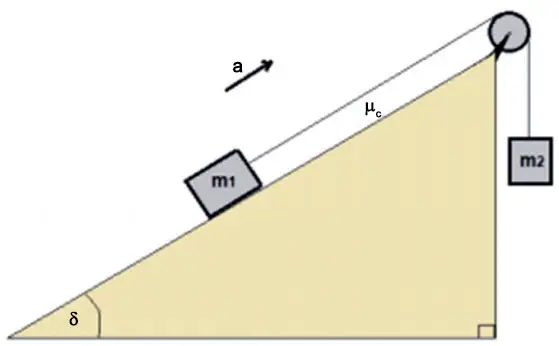
Se observan en la figura dos bloques, de masas 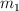 y
y 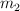 , que se encuentran unidos por una cuerda ideal (sin masa e inextensible) a través de una polea sin fricción de radio R y momento de inercia I. La superficie tiene un coeficiente de roce cinético
, que se encuentran unidos por una cuerda ideal (sin masa e inextensible) a través de una polea sin fricción de radio R y momento de inercia I. La superficie tiene un coeficiente de roce cinético 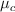 . Los bloques se mueven con una aceleración a.
. Los bloques se mueven con una aceleración a.
a) Representa en un esquema las fuerzas que intervienen sobre los objetos del sistema.
b) Determina las expresiones para calcular las tensiones en la cuerda, en función de los datos dados.
c) Calcula las tensiones con los datos: 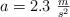 ;
; 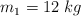 ;
; 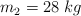 ;
; 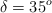 ;
; 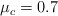 .
.
Artículos de esta sección
-
Posición del centro de masas de un sistema de cuatro partículas en el plano (7502)
Encuentra el centro de masas del sistema formado por las siguientes partículas, dadas sus masas y sus coordenadas expresadas en metros: 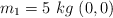 ;
; 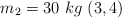 ;
; 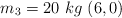 y
y 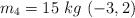 . Realiza un dibujo en el que aparezcan las masas representadas como un punto y el centro de masas con una equis.
. Realiza un dibujo en el que aparezcan las masas representadas como un punto y el centro de masas con una equis.
 Ejercicios FyQ
Ejercicios FyQ