Rueda que gira mientras está sujeta por un eje horizontal (7498)

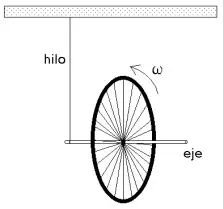
Una rueda de bicicleta se sostiene del eje con una cuerda suspendida del techo tal como muestra la figura.

El punto de amarre se ubica a una distancia de 20 cm del centro de la rueda, la llanta pesa 4 Kg y tiene un radio de 30 cm. La rueda se hace girar a 10 rev/s. El eje se orienta inicialmente de manera horizontal.

a) Demuestra que el eje de la rueda se mantendrá en posición horizontal y que esta realizará un movimiento circular.

b) Calcula la velocidad angular.

Tiempo que tarda en dar una vuelta una atracción de feria (7454)

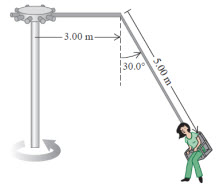
El columpio gigante de una feria local consiste en un eje vertical con varios brazos horizontales unidos a su extremo superior, como puedes ver en la figura adjunta. Cada brazo sostiene un asiento suspendido de un cable de 5.00 m, sujeto al brazo en un punto a 3.00 m del eje central.

a) Calcula el tiempo de una revolución del columpio si el cable forma un ángulo de 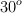con la vertical.

b) El ángulo depende del peso del pasajero para una velocidad de giro determinada?

Varilla que soporta una tensión longitudinal que provoca una deformación (7429)

Una varilla de aluminio soporta una tensión longitudinal de 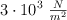y la deformación longitudinal es de 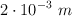. Si la varilla tiene 85 cm de longitud inicial y el modulo de Young para este material es de 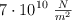, determina lo siguiente:

a) La longitud final de la varilla.

b) La magnitud de la fuerza aplicada que deformó la varilla si su sección transversal es .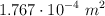

c) ¿De qué diámetro será la varilla?

Conservación de energía en un choque con coeficiente de restitución distinto de uno (7428)

Dos esferas de masas 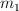y 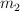están suspendidas de dos hilos paralelos de longitudes 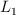y 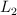respectivamente. En posición de equilibrio las esferas están con sus centros al mismo nivel. La masa 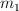se desvía lateralmente un ángulo 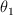y, a partir del reposo, se le deja en libertad. En su descenso choca con 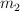y, tras el impacto se desviará un ángulo máximo 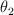. Si el coeficiente de restitución es e, determina:

a) Las velocidades de las esferas después de chocar.

b) El ángulo 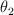que 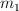se desvía tras el choque.

Tiro parabólico para impactar en un tanque con MRUA (7427)

Un mortero dispara un proyectil con una velocidad inicial 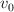formando un ángulo 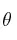con la horizontal. A 20.0 m de él un tanque parte del reposo en línea recta con una aceleración constante de 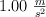. Determina la velocidad mínima inicial del proyectil para que pueda impactar en el tanque.