-
Posición del centro de masas de un sistema de cuatro cuerpos (7418)
Un sistema natural se puede modelar con un conjunto de figuras geométricas que consiste en una esfera de radio 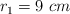 y densidad
y densidad 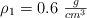 , un cilindro de radio
, un cilindro de radio 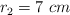 y altura
y altura 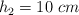 y dos esferas idénticas de radio
y dos esferas idénticas de radio 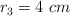 , siendo la densidad de estas tres últimas figuras geométricas
, siendo la densidad de estas tres últimas figuras geométricas 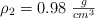 :
:
Artículos de esta sección
¿Cuál es la posición del centro de masas del sistema, respecto a los ejes de coordenadas sobre los que está representado?
-
Velocidad de los bloques de una máquina de Atwood (7406)
Dos bloques cuyas masas son 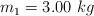 y
y 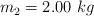 están conectados por una cuerda ligera que pasa sobre una polea sin fricción, como se muestra en la figura.
están conectados por una cuerda ligera que pasa sobre una polea sin fricción, como se muestra en la figura.
Artículos de esta sección
La polea tiene un radio R = 20.0 cm y masa M = 2.50 kg. Si el sistema se libera desde el reposo determina, usando consideraciones energéticas:
a) La rapidez de los bloques cuando el bloque 1 desciende una distancia de 5.00 m.
b) La magnitud de la aceleración de los bloques.
-
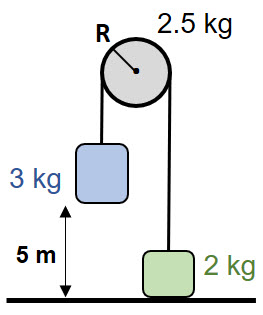
Aceleración angular de una esfera que rueda sin deslizar por un plano (7365)
Una esfera homogénea de masa M y radio R rueda sin deslizar desde el reposo hacia abajo en un plano inclinado, como se muestra en la figura.
Artículos de esta sección
Halla:
a) La aceleración angular de la esfera.
b) El mínimo coeficiente de rozamiento para evitar el deslizamiento.
-
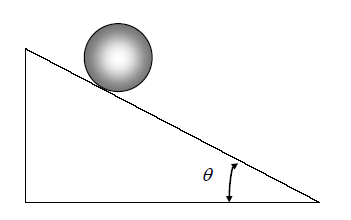
Valor de la tensión para que un pivote permanezca en equilibrio (7345)
Una barra ingrávida esta suspendida sobre un pivote tal como muestra la figura. Si el cilindro que suspende en el extremo de la barra tiene un peso de 600 N:
a) Dibuja el diagrama del cuerpo libre de la barra.
b) Escribe las ecuaciones de las condición de equilibrio.
c) Calcula la magnitud de tensión oblicua.
Artículos de esta sección
-
Momento angular de un tiovivo con un chico paseando en él (7341)
Una rueda de caballitos tiene un momento de inercia 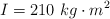 y gira alrededor de su eje vertical a
y gira alrededor de su eje vertical a 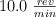 . En su borde, que dista 1.40 m del eje, está sentado un muchacho de m = 60.0 kg. Calcula el momento angular del sistema rueda-muchacho.
. En su borde, que dista 1.40 m del eje, está sentado un muchacho de m = 60.0 kg. Calcula el momento angular del sistema rueda-muchacho.
 Ejercicios FyQ
Ejercicios FyQ