-
Tensión en el cable y fuerza sobre el gozne de un sistema en equilibrio estático (7310)
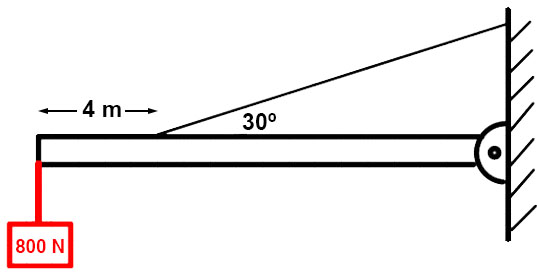
En la siguiente figura, la viga uniforme de 725 N de peso está sujeta a un pasador en el punto A:
Artículos de esta sección
a) Determina la tensión en la cuerda.
b) Calcula las componentes de la fuerza que ejerce el apoyo sobre la viga.
-
Velocidad angular de una barra homogénea cuando impacta una pelota sobre ella (7281)
Una barra metálica delgada y uniforme, de 2.00 m de longitud y con un peso de 90.0 N, cuelga verticalmente del techo en un pivote sin fricción colocado en el extremo superior. De repente, una pelota de 3.00 kg, que viaja inicialmente a 10.0 m/s en dirección horizontal, golpea la barra 1.50 m abajo del techo. La pelota rebota en dirección opuesta con rapidez de 6.00 m/s. Calcula la rapidez angular de la barra inmediatamente después del choque.
-
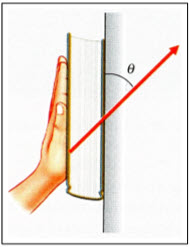
Fuerza para sujetar un libro contra la pared (7164)
Imagina que sostienes un libro contra la pared apretándolo con la mano. La fuerza forma un ángulo 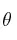 con la pared, como se muestra en la figura:
con la pared, como se muestra en la figura:
Artículos de esta sección
La masa del libro es m y el coeficiente de fricción estática es 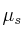 .
.
a) Calcula la magnitud de la fuerza que debes ejercer para (apenas) mantener el libro estacionario.
b) ¿Para qué valor del ángulo 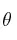 la magnitud de la fuerza requerida es la más pequeña posible? ¿Cuál es la magnitud de la menor fuerza posible?
la magnitud de la fuerza requerida es la más pequeña posible? ¿Cuál es la magnitud de la menor fuerza posible?
c) Si empujas con un ángulo mayor de 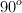 , debes hacerlo muy fuerte para sostener el libro en su lugar. ¿Para qué valor del ángulo se hará imposible sostener en su lugar al libro?
, debes hacerlo muy fuerte para sostener el libro en su lugar. ¿Para qué valor del ángulo se hará imposible sostener en su lugar al libro?
-
Alargamiento que sufren los hilos que sujetan una lámina homogénea (7150)
Una lámina uniforme de 5m de largo y 50 kilogramos de masa está sostenida horizontalmente por sus extremos mediante dos alambres verticales uno de acero (cuyo modulo de Young es 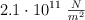 ) y otro de cobre (cuyo modulo de Young es de
) y otro de cobre (cuyo modulo de Young es de 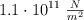 . Cada alambre tiene 3 metros de longitud y
. Cada alambre tiene 3 metros de longitud y 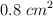 de sección transversal. Calcula el cambio de longitud de cada alambre.
de sección transversal. Calcula el cambio de longitud de cada alambre.
-
Aceleración de los bloques en una máquina de Atwood sabiendo el momento de inercia de la polea (7142)
En una máquina de Atwood, dos bloques de masas 12 y 4 kg se desplazan con una aceleración desconocida conectados mediante una cuerda ideal a través de una polea sin fricción de masa 8 kg y radio 0.2 m. Calcula la aceleración de los bloques sabiendo que el momento de inercia de la polea es 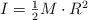 .
.
 Ejercicios FyQ
Ejercicios FyQ