Peso específico, densidad y densidad relativa del aceite que contiene un barril (8135)

Si un barril de aceite pesa 1.5 kN, calcula el peso especifico, la densidad y la densidad relativa del aceite que contiene, sabiendo que el volumen del barril es 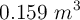y su peso es de 110 N.

Burbuja liberada por un buzo que asciende a la superficie (6395)

Un buzo libera una burbuja (esférica) de aire de 3.6 cm de diámetro desde el fondo de un lago de 14 m de profundidad. Supón que la temperatura es constante e igual a 298 K y que el aire se comporta como un gas ideal.

a) ¿De qué tamaño es la burbuja cuando alcanza la superficie.

b) Dibuja el diagrama P-V para el proceso

c) Aplicando la primera ley de la termodinámica a la burbuja, determina el trabajo que realiza el aire al elevarse a la superficie, el cambio de energía interna y el calor agregado o eliminado del aire de la burbuja conforme se eleva.

Humedad absoluta y relativa de una habitación (6116)

En una habitación de 2 000 mm de altura, 3 m de ancho y 3 m de largo se coloca un recipiente con 12 litros de agua. Al cabo de 3 horas el recipiente tiene 8 litros de agua. Calcula:

a) Humedad absoluta del aire de la habitación al cabo de 3 horas.

b) Humedad relativa en la habitación sabiendo que el ambiente puede contener un máximo 7 kg de vapor de agua en esas condiciones.

Ecuación que indica el volumen sin evaporar de un líquido en función del tiempo (5536)

Un compuesto en estado líquido, al dejar 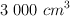a temperatura ambiente, se evapora y pierde cada día el 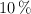de su volumen que ha quedado del día anterior.

a) Encuentra la función V(t) que describe el volumen del compuesto sin evaporar a medida que transcurre el tiempo, expresado en días.

b) En cuanto al volumen del compuesto sin evaporar, selecciona la opción correcta:

i. Se acerca a 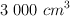, cuando t toma valores muy grandes.

ii. Es constante a partir de t = 3 000 días.

iii. Es cero cuando t = 3 000 días.

iv. Se acerca a cero cuando t toma valores muy grandes.

Tiempo de difusión de 10 pies cúbicos de hidrógeno (5175)

¿Qué tiempo tarda en difundirse 10 pies cúbicos de hidrógeno, a través de una pared porosa, si el mismo volumen de oxígeno, en las mismas condiciones, tarda 10 minutos?