pH de una disolución de un ácido triprótico y porcentaje de disociación en cada etapa (8433)

, por F_y_Q

|

Se prepara una disolución acuosa de ácido cítrico (\ce{H3C6H5O7}) con una concentración inicial de 0.05 M. El ácido cítrico es un ácido triprótico con las siguientes constantes de acidez a 25\ ^oC:

K_{a_1} = 7.4\cdot 10^{-4} ; K_{a_2} = 1.7\cdot 10^{-5} ; K_{a_3} = 4.0\cdot 10^{-7}

a) Calcula el pH de la disolución resultante, teniendo en cuenta las tres etapas de disociación.

b) Determina las concentraciones de todas las especies presentes en la disolución en equilibrio.

c) Calcula el porcentaje de cada etapa de disociación.

d) Calcula el pH de la disolución resultante después de añadirle 0.025 moles de NaOH.

P.-S.

Una manera de abordar el problema es empezar por resolver el segundo de los apartados y luego hacer el primero.

b) Al ser el ácido cítrico un ácido triprótico, puede donar tres protones cuando está en solución acuosa. Los equilibrios de disociación para cada una de las constantes de acidez son:

Primera disociación: \ce{H3C6H5O7 <=> H2C6H5O7- + H+}\ \ (K_{a_1} = 7.4\cdot 10^{-4})
Segunda disociación: \ce{H2C6H5O7- <=> HC6H5O7^{2-} + H+}\ \ (K_{a_2} = 1.7\cdot 10^{-5})
Tercera disociación: \ce{HC6H5O7^{2-} <=> C6H5O7^{3-} + H+}\ \ (K_{a_3} = 4.0\cdot 10^{-7})

Primera disociación.

La primera disociación es la más significativa debido al valor más alto de la primera constante de disociación. Debes asumir que la concentración de protones proviene principalmente de esta disociación.

\color[RGB]{2,112,20}{\bm{K_{a_1} = \frac{[\ce{H+}][\ce{H2C6H5O7-}]}{[\ce{H3C6H5O7}]}}}

Conoces la concentración inicial del ácido cítrico. Si llamas «x» a la concentración de protones y la especie diprótica tras el primer equilibrio:

7.4\cdot 10^{-4} = \frac{x \cdot x}{0.05 - x}\ \to\ \color[RGB]{2,112,20}{\bm{x^2 + 7.4\cdot 10^{-4}x - 3.7\cdot 10^{-5} = 0}}

Al resolver la ecuación de segundo grado anterior obtienes dos valores, pero solo uno de ellos positivo, que es el que debes considerar:

[\ce{H+}] = \fbox{\color[RGB]{192,0,0}{\bm{5.72\cdot 10^{-3}\ M}}}


Si quieres tener en cuenta la concentración de los iones hidróxido debidos al agua de la disolución, su concentración es:

[\ce{OH-}] = \frac{K_w}{[\ce{H3O+}]} = \frac{10^{-14}}{5.72\cdot 10^{-3}} = \fbox{\color[RGB]{192,0,0}{\bm{1.75\cdot 10^{-12}\ M}}}


Segunda disociación.

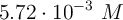
La segunda disociación contribuye menos al pH debido al menor valor de su constante de equilibrio. La concentración de protones ya es 5.72\cdot 10^{-3}\ M, por lo que la contribución de la segunda disociación será pequeña. Si haces la aproximación de que la concentración de protones no cambia de manera significativa:

K_{a_2} = 1.7\cdot 10^{-5} = \frac{(5.72\cdot 10^{-3})[\ce{HC6H5O7^{2-}}]}{5.72\cdot 10^{-3}}\ \to\ [\ce{HC6H5O7^{-2}}] = \fbox{\color[RGB]{192,0,0}{\bm{1.7\cdot 10^{-5}\ M}}}



Tercera disociación.

La tercera disociación es aún menos significativa porque su constante de disociación es la menor:

K_{a_3} = 4\cdot 10^{-7} = \frac{(5.72\cdot 10^{-3})[\ce{C6H5O7^{3-}}]}{1.7\cdot 10^{-5}}\ \to\ [\ce{C6H5O7^{-3}}] = \fbox{\color[RGB]{192,0,0}{\bm{1.19\cdot 10^{-9}\ M}}}



a) Como has supuesto que la concentración de protones no varía sustancialmente desde el primer equilibrio de disociación, el valor del pH es muy fácil de calcular:

\text{pH} = -\log[\ce{H+}] = -\log (5.72\cdot 10^{-3}) = \fbox{\color[RGB]{192,0,0}{\bf 2.24}}


c) El porcentaje de disociación en cada etapa lo calculas haciendo el cociente entre la concentración de la especie disociada y la concentración inicial del ácido, multiplicando por cien para expresarla en tanto por ciento.

Primera disociación:

\alpha_1 = \frac{5.72\cdot 10^{-3}}{0.05}\cdot 100 = \fbox{\color[RGB]{192,0,0}{\bf 11.4\ \%}}


Segunda disociación:

\alpha_2 = \frac{1.7\cdot 10^{-5}}{0.05}\cdot 100 = \fbox{\color[RGB]{192,0,0}{\bm{3.4\cdot 10^{-2}\ \%}}}


Tercera disociación:

\alpha_3 = \frac{1.19\cdot 10^{-9}}{0.05}\cdot 100 = \fbox{\color[RGB]{192,0,0}{\bm{2.4\cdot 10^{-6}\ \%}}}


d) Cuando añades NaOH, que es una base fuerte, se produce la neutralización del exceso de protones debidos al ácido cítrico. La reacción que tiene lugar es:

\color[RGB]{2,112,20}{\textbf{\ce{H3C6H5O7 + OH- -> H2C6H5O7- + H2O}}}

Al añadir 0.025 moles de NaOH, se neutralizará parte del ácido inicial, formándose una disolución tampón. Con la expresión de Henderson-Hasselbalch, considerando la primera constante de equilibrio, puedes calcular el pH resultante:

\color[RGB]{2,112,20}{\bm{pH = pK_{a_1} + log\ \frac{[\ce{H2C6H5O7-}]}{[\ce{H3C6H5O7}]}}}

Las concentraciones que forman el par conjugado son iguales, por lo que el cociente es uno:

pH = -log\ 7.4\cdot 10^{-4} + log\ 1\ \to\ \fbox{\color[RGB]{192,0,0}{\bf pH = 3.13}}