Termoquímica - EjerciciosFyQ

Artículos de esta sección

Problema de espontaniedad 0006
26 de febrero de 2010 , por F_y_Q

Calcula la variación de la energía libre de Gibbs de la combustión del metano en condiciones estándar y decide si es un proceso espontáneo.

Datos: $\Delta G^0_f(CH_4) = -50,8\ kJ/mol$ ; $\Delta G^0_f(CO_2) = -395\ kJ/mol$ ; $\Delta G^0_f(H_2O) = -237\ kJ/mol$ ; $\Delta G^0_f(O_2) = 0\ kJ/mol$
Problema de espontaniedad 0005
26 de febrero de 2010 , por F_y_Q

Calcula $\Delta G^0$ a 298 K para la reacción:

$H_2\ (g) + Cl_2\ (g)\ \to\ 2\ HCl\ (g)$

¿Cuáles son las contribuciones de H y S a la espontaneidad de la reacción?
Problema de espontaniedad 0004
26 de febrero de 2010 , por F_y_Q

Calcula $\Delta H^0$ , $\Delta S^0$ y $\Delta G^0$ e indica si es espontánea la siguiente reacción a 298 K:

$Fe_2O_3\ (s) + 3\ C\ (s)\ \to\ 2\ Fe\ (s) + 3\ CO\ (g)$

| 2
Variación de la energía libre de Gibbs para dos reacciones (521)
26 de febrero de 2010 , por F_y_Q

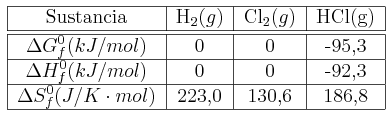
Calcula el incremento de energía libre estándar para las siguientes reacciones:

$a)\ \ce{2NaF(s) + Cl2(g) -> F2(g) + 2NaCl(s)}$

$b)\ \ce{PbO2(s) + 2Zn(s) -> Pb(s) + 2ZnO(s)}$

Comenta qué piensas sobre la posibilidad de utilizar estas reacciones en la obtención de flúor y plomo respectivamente. Datos:

$\begin{tabular}{| c | c | c | c | c | } \hline Sustancia&NaF&NaCl&\ce{PbO2}&ZnO\\\hline \Delta H_f^0\ (kJ\cdot \text{mol}^{-1})&-569&-411&-276&-348\\\hline \Delta S_f^0\ (J\cdot \text{mol}^{-1}\cdot K^{-1})&58.6&72.4&76.6&43.9\\\hline \end{tabular}$

Ver solución paso a paso

| 2
Determinación de la espontaneidad de la descomposición del monóxido de nitrógeno (520)
25 de febrero de 2010 , por F_y_Q

La descomposición del monóxido de nitrógeno transcurre según:

$\ce{N2O(g) -> N2(g) + \textstyle{1\over 2}O2(g)}$

Siendo $\Delta S^0 = 75.2\ J\cdot K^{-1}$ y $\Delta H^0 = 43.9\ kJ\cdot mol^{-1}$ .

a) ¿Es la reacción espontánea en condiciones estándar?

b) ¿A partir de qué temperatura será espontánea?

Ver solución paso a paso