-
Velocidad y aceleración de un móvil en función del tiempo (8457)
Un móvil describe una trayectoria en el plano XY dada por el vector de posición, expresado en unidades SI:
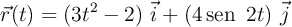
a) Determina los vectores velocidad y aceleración en función del tiempo.
b) Calcula los vectores velocidad y aceleración en el instante 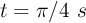 .
.
c) Halla el módulo de la velocidad y de la aceleración en 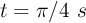 .
.
-
Posición, velocidad, momento lineal y aceleración del centro de masas de un sistema de dos partículas (8415)
Un sistema de dos partículas de masas 2 y 3 kg se mueven en el plano XY. En un instante dado, las posiciones y velocidades de las partículas son:
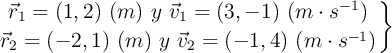
a) Calcula la posición del centro de masas (CM) del sistema.
b) Determina la velocidad del centro de masas.
c) Calcula el momento lineal total del sistema.
d) Determina el momento angular total del sistema respecto al origen.
e) Si las partículas están sometidas a las fuerzas externas 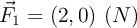 y
y 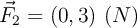 , calcula la aceleración del centro de masas.
, calcula la aceleración del centro de masas.
-
Momento de inercia de un sistema de dos esferas unidas por un hilo (8377)
Dos masas puntuales 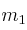 y
y 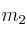 están separadas por una barra sin masa de longitud L:
están separadas por una barra sin masa de longitud L:
a) Deduce una expresión para el momento de inercia del sistema, respecto a un eje perpendicular a la barra y que pasa por un punto situado a una distancia 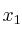 de la masa
de la masa 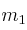 .
.
b) Calcula la variación del momento angular con la distancia y demuestra que es mínima cuando el eje pasa por el centro de masas del sistema.
-
Lanzamiento parabólico en un partido entre Brasil y Argentina (6389)
En un partido amistoso de fútbol entre Argentina y Brasil, cuando estaban empatados a uno y en el minuto 90, el árbitro pita una falta a favor de Brasil alejada 32 m de la portería. El jugador que la lanza es capaz de imprimir una velocidad de 30 m/s a la pelota y la barrera de los jugadores argentinos, de una altura media de 1.80 m, se sitúa a 12 m del punto de lanzamiento. Determina:
a) ¿Cuál debe ser el ángulo del lanzamiento para colocar el balón en la esquina superior izquierda sin que la barrera obstruya el lanzamiento?
b) ¿Cuál debe ser el ángulo del lanzamiento para colocar el balón en la esquina inferior izquierda sin que la barrera obstruya el lanzamiento?
-
Centro de masas de un sistema formados por dos barras soldadas (8107)
Se sueldan, una a continuación de otra, dos varillas homogéneas A y B de la misma longitud «L», pero hechas de dos materiales diferentes, siendo la densidad de A doble que la de B. ¿A qué distancia del extremo de A se encuentra el centro de masas del sistema?
 Ejercicios FyQ
Ejercicios FyQ