Cinemática, dinámica y estática

(#6293) Seleccionar

Estudio de un muelle que gira formando un péndulo cónico (6293)

Un cuerpo de 1 kg de masa y dimensiones pequeñas está unido a un muelle de masa despreciable que tiene una longitud natural de 48 cm y una constante elástica de 980 N/m. Hacemos girar el muelle y el cuerpo que sostiene, como un péndulo cónico, a una frecuencia de 60 rpm, manteniendo fijo el extremo que no está unido al cuerpo.

a) Determina el alargamiento del muelle y el ángulo que forma el eje de rotación del sistema con la dirección del muelle, cuando está girando.

b) Tomando como origen (o cero) de energía potencial gravitatoria el plano horizontal que contiene el punto fijo del muelle, calcula la energía mecánica total del sistema.
(#6243) Seleccionar

Volumen mínimo de una boya para mantener en equilibrio un bloque de latón en agua (6243)

Un cubo de latón de 6 in de arista y 39.4 kg de masa se desea mantener en equilibrio bajo el agua sujetándolo a una boya de espuma. Si la espuma de la boya tiene una densidad de 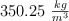$350.25\ \textstyle{kg\over m^3}$ , ¿cuál es el volumen mínimo requerido de la boya?

Considera que la densidad del agua es 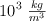$10 ^3\ \textstyle{kg\over m^3}$ .
(#6159) Seleccionar

Posición, velocidad y momento angular de un sistema de dos partículas distintas (6159)

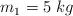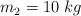Las partículas $m_1 = 5\ kg$ y $m_2 = 10\ kg$ tienen movimientos independientes. La partícula 1 se deja libre sobre el plano liso, inclinado un ángulo 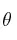$\theta$ , mientras que la partícula 2 se lanza verticalmente hacia abajo desde la altura h con una velocidad inicial de 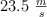$23.5 \ \textstyle{m\over s}$ . La partícula 2 inicia su movimiento en el instante en que la partícula 1 abandona el plano inclinado. Determina, para t = 2 s después de que la partícula 1 abandona el plano inclinado:

a) La posición del centro de masas del sistema constituido por 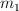$m _1$ y $m _2$ .

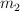b) La velocidad del centro de masas.

c) El momento angular de cada partícula respecto al origen del sistema de referencia.

Artículos de esta sección
(#6158) Seleccionar

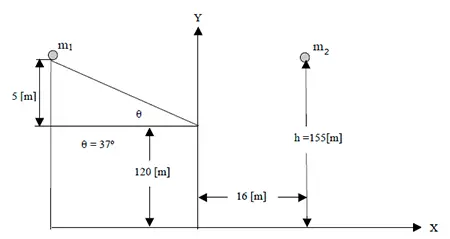
Posición, velocidad y momentos angular y lineal de un sistema de dos partículas (6158)

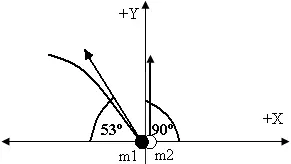
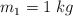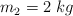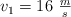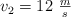La figura muestra un sistema formado por dos partículas con masas $m_1 = 1\ kg$ y $m_2 = 2\ kg$ . Las partículas se lanzan simultáneamente y sus velocidades iniciales son $v_1 = 16\ \textstyle{m\over s}$ y $v_2 = 12\ \textstyle{m\over s}$ . Para el instante t = 2 s, determina:

a) La posición del centro de masas del sistema respecto al origen.

b) La velocidad del centro de masas del sistema respecto al origen.

c) El momento angular del sistema respecto al origen.

d) El momento lineal de la partícula 1 respecto al centro de la masas.

Artículos de esta sección
(#6025) Seleccionar

Velocidad, rapidez y posición de una partícula a partir de su aceleración (6025)

En t = 0, una partícula parte del reposo en x = 5 m e y = 8 m, y se mueve en el plano XY con una aceleración de 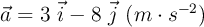$\vec{a} = 3\ \vec{i} - 8\ \vec{j}\ (\textstyle{m\cdot s^{-2}})$ . Determina:

a) Las componentes X e Y de la velocidad en t = 4 s.

b) La rapidez de la partícula en t = 4 s.

c) La posición de la partícula en t = 8 s.