Análisis vectorial de un choque perfectamente inelástico de tres masas distintas (5986)
Tres partículas de masas 3m, 2m y m, con celeridades 3v, 2v y v, respectivamente, confluyen en un punto como se muestra la figura. La partícula 1 se mueve con una velocidad paralela al eje X, mientras que las partículas 2 y 3 se mueven con velocidades en las direcciones determinadas por los ángulos 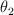 y
y 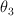 , como se muestra en la figura. Después de la colisión las tres partículas permanecen unidas.
, como se muestra en la figura. Después de la colisión las tres partículas permanecen unidas.
a) Determina analíticamente, y en función de las variables suministradas en el enunciado, el momento total antes del choque, expresado vectorialmente en términos de los vectores unitarios 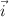 y
y 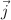 .
.
b) La velocidad final, expresada vectorialmente en términos de los vectores unitarios 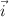 y
y 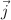 , de las partículas unidas después del choque.
, de las partículas unidas después del choque.
Para el conjunto de valores m = 5.70 kg, v = 7.30 m/s, 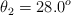 y
y 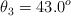 , determina numéricamente:
, determina numéricamente:
c) Los resultados obtenidos los apartados a) y b).
d) La dirección de la velocidad final de las masas unidas.

Artículos de esta sección
Coeficiente de rozamiento y ángulo de un plano inclidano rugoso (5975)
Un bloque de madera de 4.0 kg se coloca sobre un plano inclinado rugoso. Si sabemos para que un ángulo de 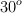 el bloque cae con una aceleración de
el bloque cae con una aceleración de 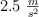 , calcula:
, calcula:
a) El valor del coeficiente de rozamiento entre el bloque y el plano inclinado.
b) El ángulo que debe tener el plano inclinado para que el bloque baje con velocidad constante, suponiendo ahora que 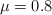 .
.
 Ejercicios FyQ
Ejercicios FyQ